This blog is part of our RELevant series, which provides viewpoints and findings from REL Mid-Atlantic.
For the first time in three years, states across the country are identifying low-performing schools under the Every Student Succeeds Act (ESSA). One of the long-recognized technical challenges in this process involves the reliability of the measures of school performance. Every performance measure has some random variation, but states want to identify the schools that really need support and improvement rather than those that had bad luck. Random variation increases as the number of students shrinks, which is especially problematic for the measures of subgroup performance that are used to identify schools for targeted support and improvement (TSI) or additional targeted support and improvement (ATSI).
Minimum group sizes avoid random error for small subgroups—at a cost
Recognizing this problem, ESSA allows states to set thresholds for the minimum number of students in a subgroup to be used for accountability (often called minimum “n-sizes”). States hold schools accountable for the performance of a subgroup only if the subgroup includes enough students to meet the minimum n-size threshold (ranging from 10 to 30 students). The minimum n-size threshold prevents random errors for small subgroups, but it involves a tradeoff: Students who are members of smaller subgroups are omitted from subgroup accountability rules, undermining ESSA’s commitment to equitable outcomes for all student groups. One analysis found that with an n-size threshold of 30 students, nearly 40 percent of Black elementary-grade students nationwide could be omitted from subgroup accountability. A REL study from 2020 found that low-performing subgroups are often overlooked just because they don’t have quite enough students to meet n-size thresholds.
Bayesian stabilization can reduce random error without ignoring small subgroups
Working with the Pennsylvania Department of Education, we’ve found a happy solution to this dilemma. Bayesian stabilization could allow states to reduce random error in subgroup (and schoolwide) performance measures even while reducing minimum n-sizes, if they choose to do so. In a new white paper, we use Bayesian statistical methods with subgroup-level data for schools across Pennsylvania to increase accuracy and reduce random error in subgroup proficiency rates. Bayesian methods increase accuracy by incorporating contextual information—such as from the subgroup’s historical performance or from subgroups in other schools across the state—to improve the measure of each individual subgroup’s performance. Our report shows that Bayesian stabilization substantially reduces the random variability of subgroup performance, especially for small subgroups.
Below I’ve pasted a chart from our report that compares the variability (as measured by standard deviation) of subgroup proficiency rates for subgroups of different sizes, with and without stabilization. Smaller subgroups are on the left, with the subgroup size increasing to the right. The darker bars show the variation in the original, unstabilized proficiency results. As expected, in the unstabilized results the smaller subgroups have more random error and therefore higher variability than larger subgroups. This means smaller subgroups will be more likely to end up with particularly low (or high) scores due to luck rather than true performance. And that could cause a state to identify the wrong schools for TSI or ATSI.
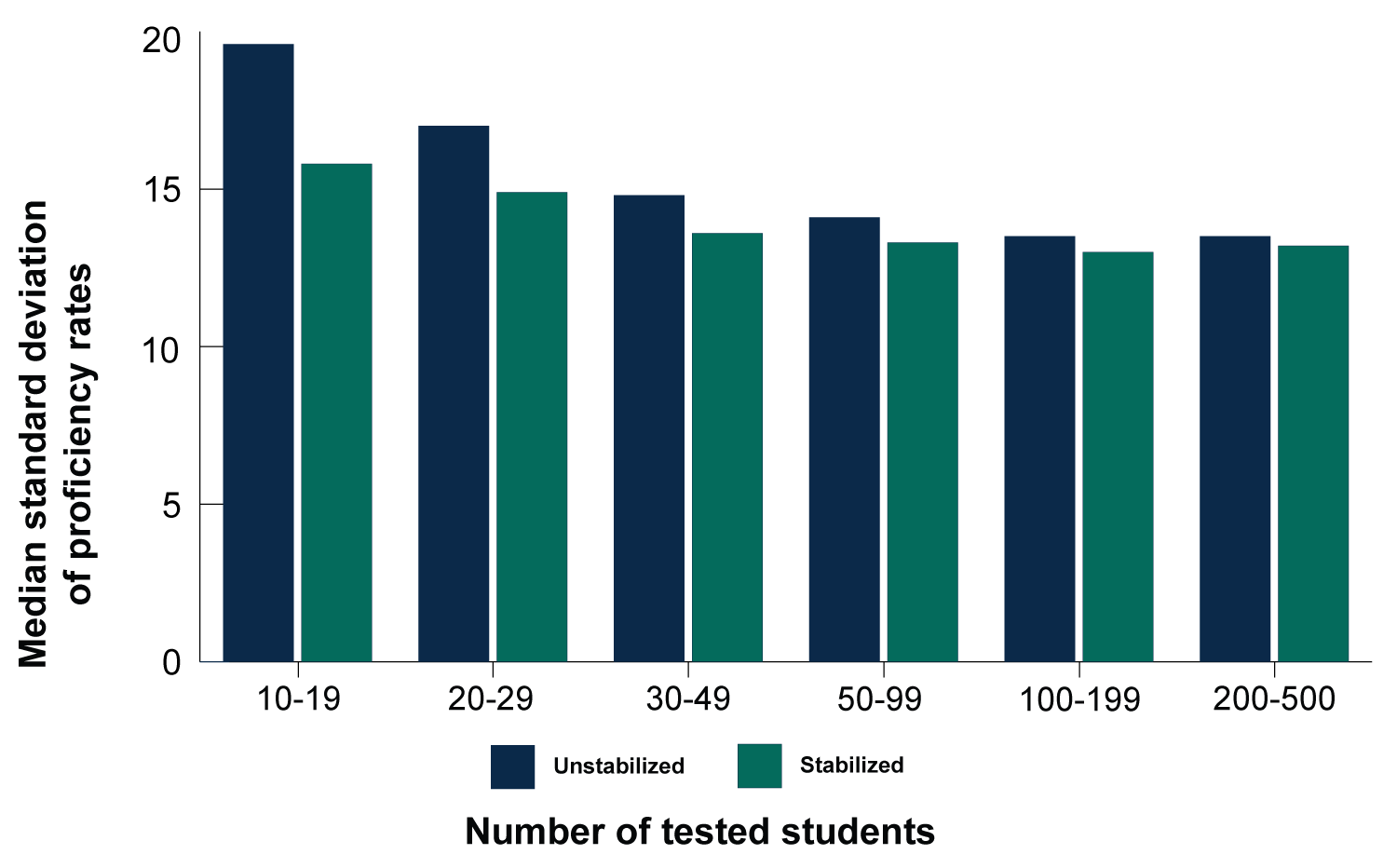
Figure 1: Stabilization substantially reduced the variability of proficiency rates for small subgroups, making the median standard deviation relatively constant across sample size categories.
Note: The figure shows the median across subgroups of the standard deviation calculated across schools of a certain sample size within a subgroup for the 2018/19 year. For example, included in the left-most bar are the standard deviation of proficiency rates across subgroups of economically disadvantaged students with only 10–19 test-takers, along with the standard deviations of proficiency rates in other subgroups with only 10–19 test-takers, separately by subgroup. The median standard deviation across subgroups for the 10–19 sample size category is plotted in the figure.
Source: Pennsylvania Department of Education data.
The green bars in the figure show the (Bayesian) stabilized results, which have less variability in every group size than the unstabilized results. Stabilizing reduces random error across the board. Moreover, the variability of the stabilized results increases only slightly as the subgroup size shrinks. Stabilization makes a bigger difference for smaller subgroups—exactly what is needed, since the smaller subgroups had more random error before stabilization. As a result, the distribution of stabilized results for small subgroups is not much wider than the distribution for larger subgroups. Stabilization substantially reduces the role of bad luck in getting a school identified for TSI or ATSI.
Indeed, it is worth noting that stabilized subgroups with only 10-19 students have lower variability than unstabilized larger groups of 20-29 students. Similarly, stabilized subgroups of 20-29 students have variability that is equivalent to that of unstabilized subgroups of 30-49 students. At these subgroup sizes, this suggest that stabilization is better than an n-size minimum at reducing random error.
The best of both worlds: equitable accountability with reliability
One positive implication of these results is that Bayesian stabilization could give states the opportunity to have their cake and eat it too: It is possible to reduce minimum n-size thresholds (from 30 to 20 or from 20 to 10) while increasing the stability of the measure. In other words, more students can be included in subgroup accountability measures—consistent with a commitment to equity—even while reducing the risk that a school would be identified for improvement based on bad luck alone.
Regardless of whether states choose to reduce minimum n-size thresholds, Bayesian adjustments can improve the reliability of their subgroup performance measures, making it more likely that states identify the schools that actually need support and improvement the most. And that’s what school accountability systems are supposed to do.
Cross-posted from the REL Mid-Atlantic website.